| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 스케줄러
- 데이터베이스
- 컴파일러
- React
- 정보검색
- css
- C언어
- 파싱테이블
- 데이터분석
- 가상메모리
- 오픈소스웹소프트웨어
- 언어모델
- 웹소프트웨어
- 객체지향설계
- 클래스
- 836
- 프로세스
- 랩실일기
- DB
- 도커
- OS
- docker
- 파싱
- 컴파일
- 자료구조
- 운영체제
- NLP
- 소프트웨어공학
- Linear Algebra
- 자연어처리
- Today
- Total
observe_db
[정보검색]4. Index Construction 본문
2. Introduction
정보 검색은 HW의 제약조건에 기반한다.
메모리가 디스크(HDD)보다 빠르지만(10^3~10^6정도), 용량이 작다.
때문에 페이징 등의 기법으로 디스크에서 정보를 가져와야하는데,
Disk는 회전/탐색에 시간이 걸리지만, Block 단위로 한번에 큰 범위를 가져오는게 가능하다.(8KB~256KB)
RCV1 collection
- 로이터 통신 collection
- 기사 제목과 짤막한 내용으로 구성된다.
- 기사 개수:800K
- 기사당 토큰 수 200
- term 수 400K(보통 큰 범위는 500K정도)
- 토큰당 바이트 6(공백 등 포함)/4.5(공백 등 제외)
- term 당 바이트 7.5(*토큰에서 짧고 자주 나오는 단어로 인해 평균이 내려감)
- non-positional posting 100M
3. BSBI algorithm
이전에 봤던 inverted index (non-positional)을 만드는 과정을 복기해보자.
- document 내의 모든 term들을 쭉 뽑아내서
- term들에 docId를 붙이고
- 그것을 term의 오름차순으로 정렬해서
- 같은 단어들을 묶어서 posting을 만든다.
3번 과정에서 정렬을 해야하는데, 만약 메모리에 모두 적재할 수 없다면?
external sorting(->merge sort)을 해야한다.
큰 흐름은
block 안에서 posting을 계산하고->block을 병합(Merge)하여 메모리에서 정렬하고->디스크에 쓰는 것
위 과정을 반복한다.
4. SPIMI algorithm
이전 정렬-기반 알고리즘의 단점: 디렉토리 만드는 데에 한번, 병합에 한번 총 두번의 스캔이 필요함.
그래서 Single-pass in-memory indexing(SPIMI)
- 주요 아이디어 1: 각 블록에 나누어진 dictionary들 생성-block에 termID 매핑 필요 없음
- 주요 아이디어 2: 정렬하지 않음. posting list의 posting은 발생한 순서대로.
- 그렇게 생성된 각 index들을 하나의 큰 index로 병합
Compression
- term의 압축
- posting 압축
- 다음 챕터에서 ..
5. Distributed indexing(분산 인덱싱)
web-scale 인덱싱은 반드시 분산 컴퓨터 클러스터를 사용한다.(규모)
그런데, 개별 컴퓨터 중 하나가 결함(fault-prone)이 있다면?
예~전 구글의 경우(2007년쯤)
99.9%로 노드 컴퓨터가 살아있고, 1000개의 컴퓨터가 있을 때에
이 모든 시스템이 돌아갈 가능성은 약 37%(0.367...)
분산 인덱싱
master를 안전하다 간주되는 인덱싱 작업에 유지.
인덱싱을 각자의 병렬 작업 집합으로 분리.
상태에 맞는 최적의 머신에 할당.
병렬 작업은 두가지 집합으로 정의할 수 있다.
- Parser
- Inverter
입력 document collection을 split들로 나눈다.(BSBI나 SPIMI의 블록)
각 split은 document의 부분집합.
Parser
- Master가 split를 이상적인 parser에 할당함
- Parser는 문서(document)를 한번에 읽고 (term, docID)-짝을 출력한다.
- j-term-partition으로 짝을 쓴다.
- 각 다양한 term들의 첫 글자에 해당
Inverter
- 모든 (term, docID) 짝(=posting)을 하나의 term-partition으로 모은다.
- 정렬하고 posting list에 쓴다
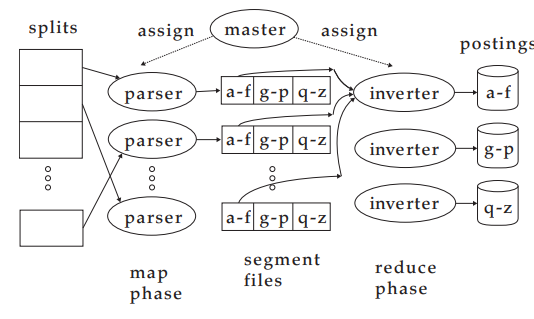
MapReduce
위의 알고리즘이 MapReduce의 예시
분산 컴퓨팅을 위한 강력하고 개념적으로 간단한 프레임워크(+배포 코드 작성 필요X)
한 단계로 인덱스 구축. 다른 단계로 term-partition을 document-partition으로 변환.
6. Dynamic indexing
collectio들은 정적(static)
아주 가끔 Document들이 추가/삭제/수정 됨.
=>dictionary와 posting도 수정해야함.(dynamically modified)
가장 간단한 방법
- 큰 main 인덱스를 디스크에 유지
- 새로운 docs는 작은 보조 인덱스로 메모리에
- 양쪽을 비교하며 결과를 병합.
- 주기적으로 보조 인덱스를 큰쪽에 병합
- 삭제?
- 삭제된 docs의 bit-vector를 무효로한다.
- 이 bit-vector를 이용하여 인덱스 별로 반환되는 docs를 필터링
- 단점: 자주 병합함. 병합 중에는 탐색 성능이 안좋음.
대수적 병합(Logarithmic merge)
- 인덱스 병합 비용을 경과 시간에 따라 상환
- index의 series를 유지. 이전보다 2배 커짐.
- 가장 작은 Z0을 메모리에 유지
- 더 큰 것들(I0 I1..)은 디스크에
- Z0가 너무 크면 I0처럼 디스크에 쓰거나 or I0와 병합(이미 있는 경우)
- 인덱스의 수는 O(log T)로 제한된다.(T: 읽을 수 있는 posting의 총 수)
- 즉 O(log T)개의 인덱스를 병합하는 것이 필요하다
- 시간 복잡도는 O(T log T): T번 O(log T)를 시행.
- 부분 인덱스: 인덱스 구성 시간은 O(T^2): a+2a+3a.... +na = a*(n*(n+1)/2) = O(n^2)
- 이게 더 효율적
종종 combination은
- 변화 빈번
-스왑이 가능한 인덱스의 큰 부분을 회전(rotation)
- 때때로 완전한 rebuild
positional index: 기본적으로 중간 데이터 구조가 크다는 점을 외에는 동일한 문제
'학교 공부 > 정보검색(4-2)' 카테고리의 다른 글
| [정보 검색] 6. Scoring, Term Weighting, The Vector Space Model (1) | 2024.11.01 |
|---|---|
| [정보 검색] 5. Index Compression (2) | 2024.10.18 |
| [정보검색] 3. Dictionaries and tolerant retrieval (0) | 2024.10.11 |
| [정보검색] 2. The term vocabulary and postings lists (1) | 2024.10.06 |
| 1. Boolean Retrieval (0) | 2024.10.03 |



