| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- OS
- 컴파일
- Linear Algebra
- 정보검색
- 언어모델
- 자료구조
- React
- 데이터베이스
- 자연어처리
- 소프트웨어공학
- css
- 파싱
- C언어
- 클래스
- 운영체제
- 파싱테이블
- 컴파일러
- 랩실일기
- DB
- NLP
- 객체지향설계
- 스케줄러
- 836
- 프로세스
- 가상메모리
- docker
- 오픈소스웹소프트웨어
- 도커
- 데이터분석
- 웹소프트웨어
- Today
- Total
observe_db
[NLP] 12. n-gram 언어 모델 본문
언어모델(Language Model, LM)
: 언어의 구성 요소에 확률 값을 부여하여 다음 구성요소를 예측하거나 생성하는 모델
언어 구성요소: 글자, 형태소, 단어, 단어열(문장), 문단
기본적으로 주어진 단어를 바탕으로 다음 단어(또는 그 조합)를 예측하는 일
다양한 자연어 처리 문제를 해결하기 위한 기초로 활용
통계적 언어 모델(Statistical Language Model)
: 단어열이 가지는 확률 분포 기반으로 각 단어 조합 예측
주어진 단어를 기반으로 확률이 가장 높은 다음 단어를 예측
문장 생성에 이용 가능
ex. n-gram 언어 모델
조건부 확률의 연쇄 법칙(chain rule)을 이용하여 단어 조합(문장)의 등장 확률 예측.
학습 말뭉치 내에서 각 단어의 조합이 나오는 횟수에 기반하여 확률 계산
모든 단어 조합 확률을 계산해야하므로 계산 복잡도가 높고 방대한 양의 말뭉치가 필요
실제 모든 단어 조합을 나타내는 것은 현실적으로 불가능.
마르코프 가정을 이용해 복잡성을 해결하고 간소화.
- 미래 사건에 대한 조건부가 과거에 대해서 독립, 현재 사건에만 영향을 받는다고 가정.
n-gram 언어모델
-특정 단어가 주변에 있는 n개의 단어(n-gram)와 연관된다고 가정.
수식

확률 추정

<s>와 </s>로 시작/끝 표시
평가

n이 커질수록 일정 수준까지는 PPL이 감소
문제점
n-gram의 한계
- 생성된 문장이 부자연 스러움+기존과 유사
- 학습 corpus에 따라 확률값 차이
- corpus의 양
희소성 문제
- 학습되지 않은 새로운 데이터에 대한 예측을 못함(확률이 0이니까)
- 모든 삼라만상을 담는건 불가능(aka. 충주맨)
- 한정된 학습 말뭉치 내에서 모델의 일반화가 필요
마르코프 가정의 문제
- 단어의 등장확률이 주변 n단어에만 의존적일까? 장기의존성 간과함.
평탄화/스무딩(Smoothing)
:학습 말뭉치 내의 존재하지 않는 단어 조합에 대해 특정 값(α)을 부여
확률 분포에 약간의 변화를 주는 방법
일반적으로 [0,1]의 범위에서 부여
존재하지 않는 단어열로 전체 문장의 확률이 0이 되는것 방지
V는 말뭉치에 등장하는 단일 단어 개수 의미.
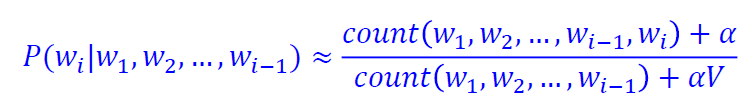
일반화 방법-보간법(interpolation)
-특정 n-gram 확률을 이전 n-gram확률과 섞음
일정 비율 가중치를 각각 곱하여 합
일반화 방법-백오프(backoff)
신경망 n-gram 모델
단어를 벡터로->이 벡터를 신경망에 넣어 계산, 단어 예측
저장 공간 불필요/데이터 평탄화 유리/문맥 한계는 있음
RNN 기반
-은닉층 출력을 다시 입력으로
-n gram의 한계는 해결
-먼거리의 정보는 상실->LSTM, GRU 사용으로
ATTENTION(주의 집중)
먼거리 정보 처리
정보 병목 해결
직렬처리라 느림.
'학교 공부 > 자연언어처리(4-2)' 카테고리의 다른 글
| [NLP] 15. 프롬프트 및 순화 학습 (1) | 2024.12.04 |
|---|---|
| [NLP] 14. 거대 언어 모델(LLM) (0) | 2024.11.28 |
| [NLP] 11. 단어 벡터 (1) | 2024.11.08 |
| [NLP] 10. 기계번역 (0) | 2024.11.08 |
| [NLP] 9. 정보 추출 (0) | 2024.11.01 |



